For our second project, we used linear regression to investigate predictions relating to the movie industry. My initial idea centered around trying to predict the quality of a movie. In some ways, predicting the IMDB Rating or Metacritic score of a movie isn't entirely useful, as those ratings will nearly always be available as soon as the movie is released, but if we could make a model without using any time sensitive inputs, we could use it to estimate the hypothetical rating of any combination of director/actors.

My initial idea was to use career averages for all the major players involved - director, writer, and cast, to see if there was a correlation between their previous body of work and their upcoming films. So, if it was someone's third film, their "score" would be the average imdbrating of their first two films, if it was their 10th, I used the average of their first 9. I gave some thought to weighting recent films higher than older ones, as its possible they would have more relevance to the quality of the next film produced, but ultimately decided to stick with the unweighted career average.

This presented a problem when training the model, because if this was the first film for any of the major players, they didn't have an average score and I couldn't use them to train the model. One way around this would have been to use a scoring system instead of a mean- for example, all directors would start at 0, and each time they create a top rated movie, they would get, say 5 points, while a below average movie would cause them to lose 5 points, and an average movie would leave their score unchanged.

A better solution, which I unfortunately did not have time to implement, would be to train multiple regression models- one to predict the imdb rating of a movie, and another to predict the imdbrating of the director, given the ratings of the other actors and writer. Similar models could be made for all inputs, so that if we wanted to predict the rating of a movie directed by Martin Scorcese, starring Brad Pitt, Matt Damon, and Andrew Sherman-Ash, we would first estimate Sherman-Ash's IMDB Rating, then use it as input in the original model to estimate the movie's rating.

The following is a correlation matrix of selected features versus IMDB Rating:

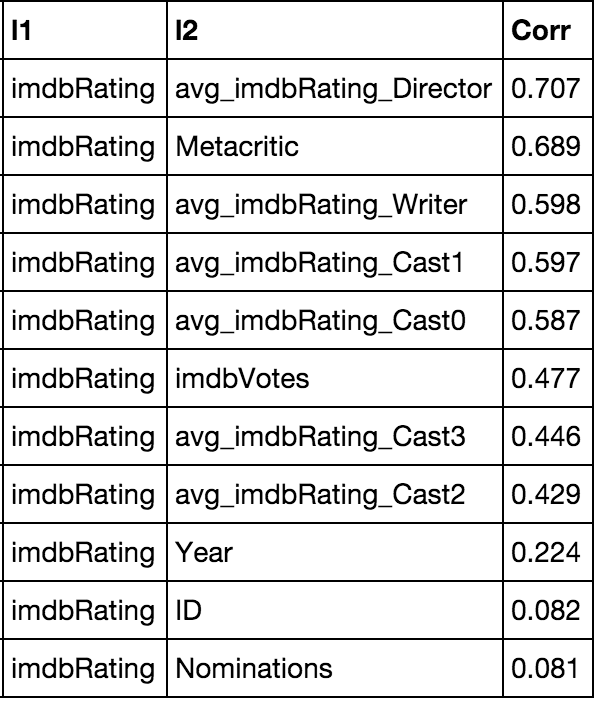
As we suspected, the average career ratings of the director and lead actors have a significant impact on the eventual IMDB Rating of the film. We can see that Metacritic rating and IMDB Votes are also highly correlated, but we can't use those features for our model, since once we know the Metacritic rating or number of votes for a movie, the IMDB Rating (what we are trying to predict), would already be known publicly. Another possibly interesting note here is that the number of oscar nominations has almost no correlation with the rating- maybe the qualities valued in a movie differ greatly between IMDB voters and the Academy.

Below are scatter plots for director and lead actor:

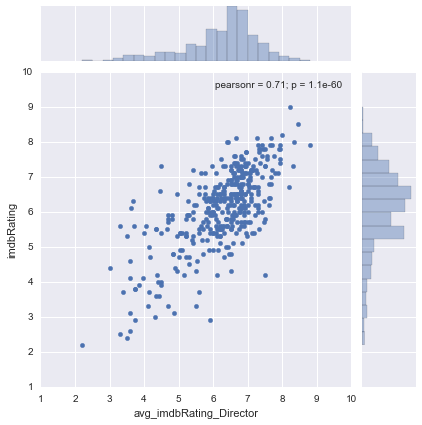
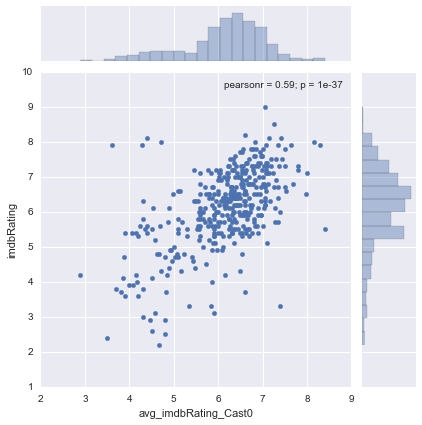
The model does a decent job predicting IMDB Rating, using only director, cast0, cast1, and cast3. It's interesting that cast3 (the 4th listed actor) makes the cut, while cast2, and writer had nearly no effect on the model. This could be because cast3 better captures the depth of the cast, or because the effects of the writer and 3rd cast member are already captured among the other features.

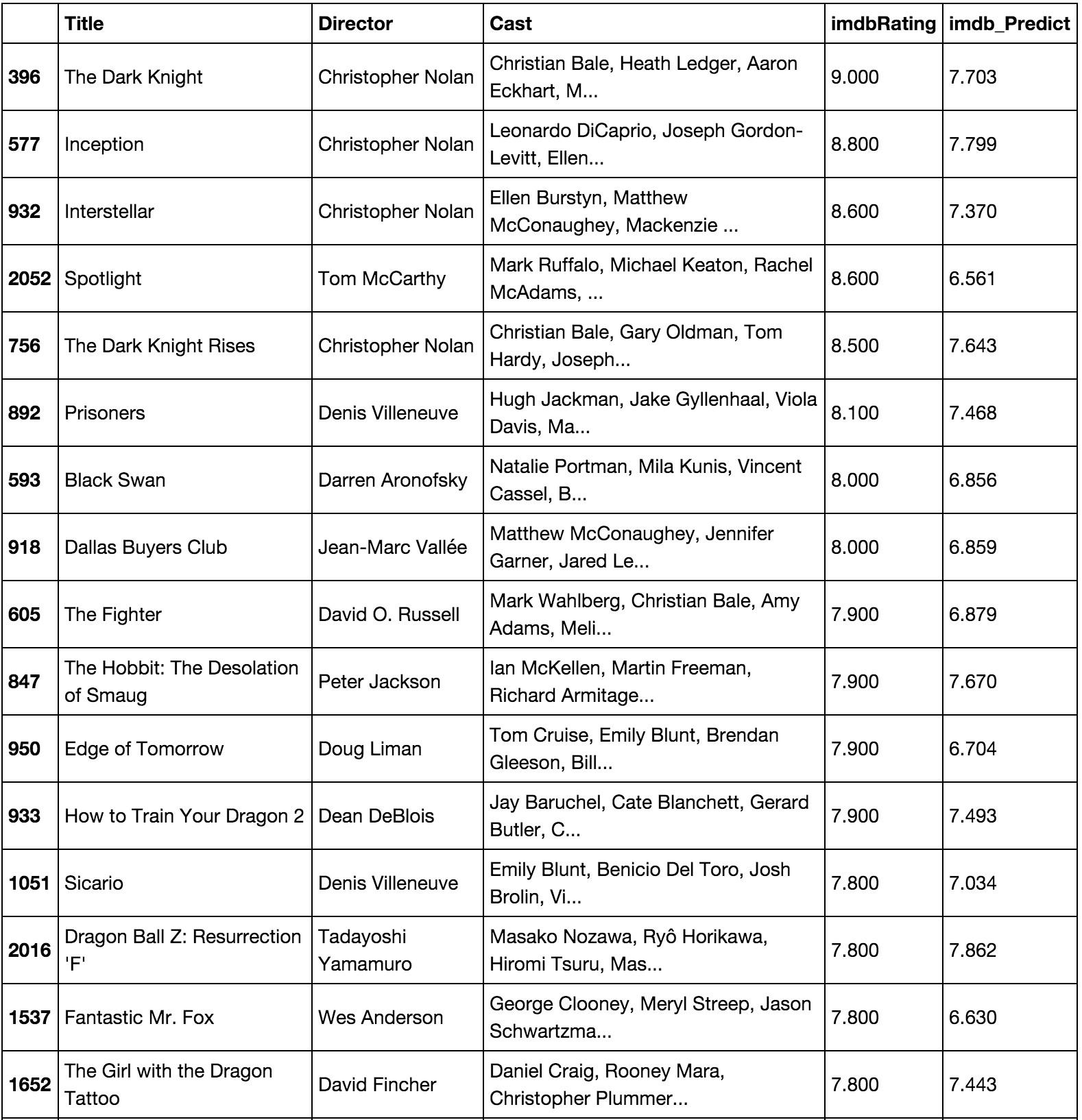
Here is a subset of top ranked recent movies on imdb, along with their ratings as predicted by the model (Chris Nolan 1-2-3-5!)

And here are the model's top predicted movies (sorry Noah!):

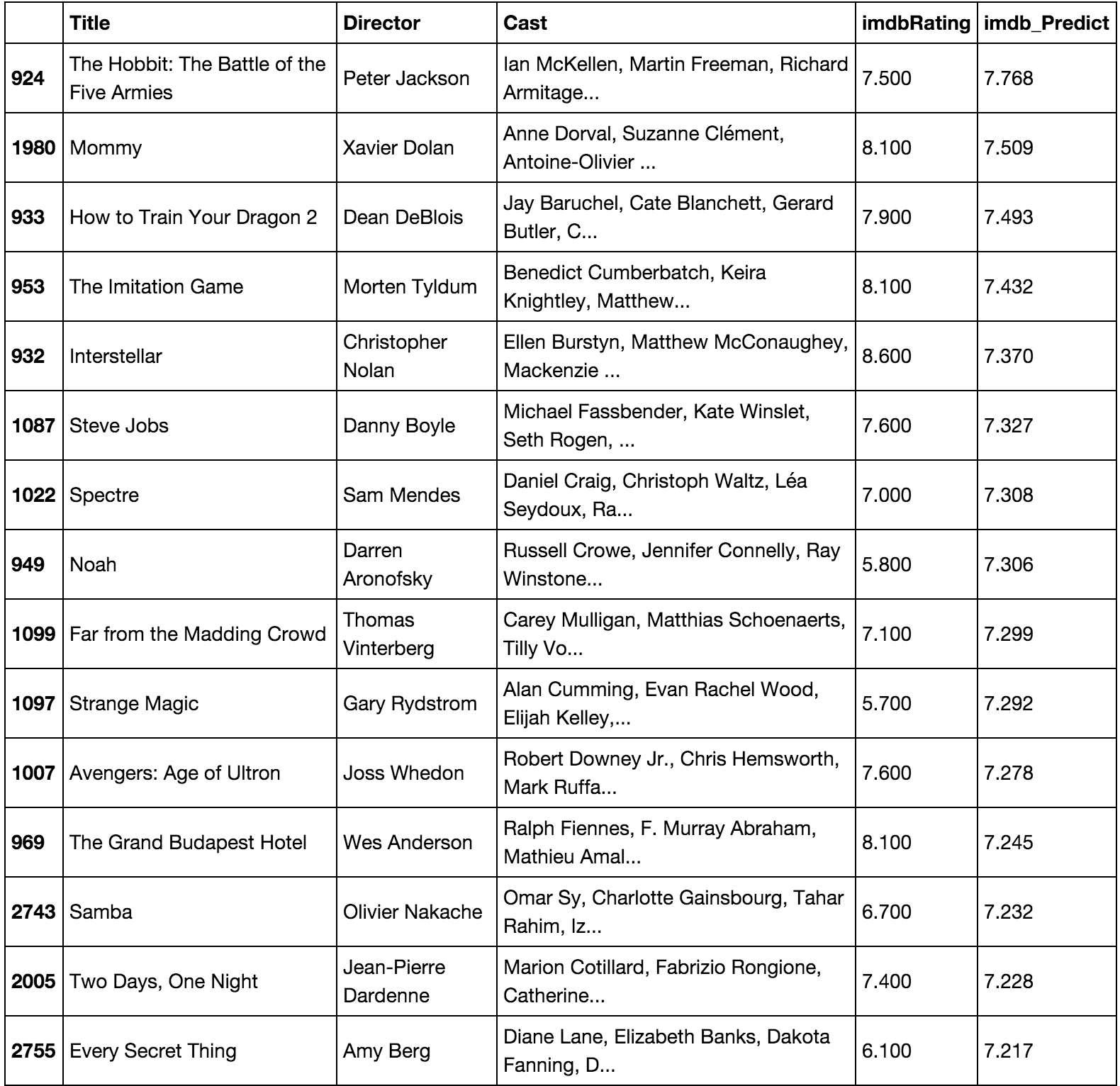
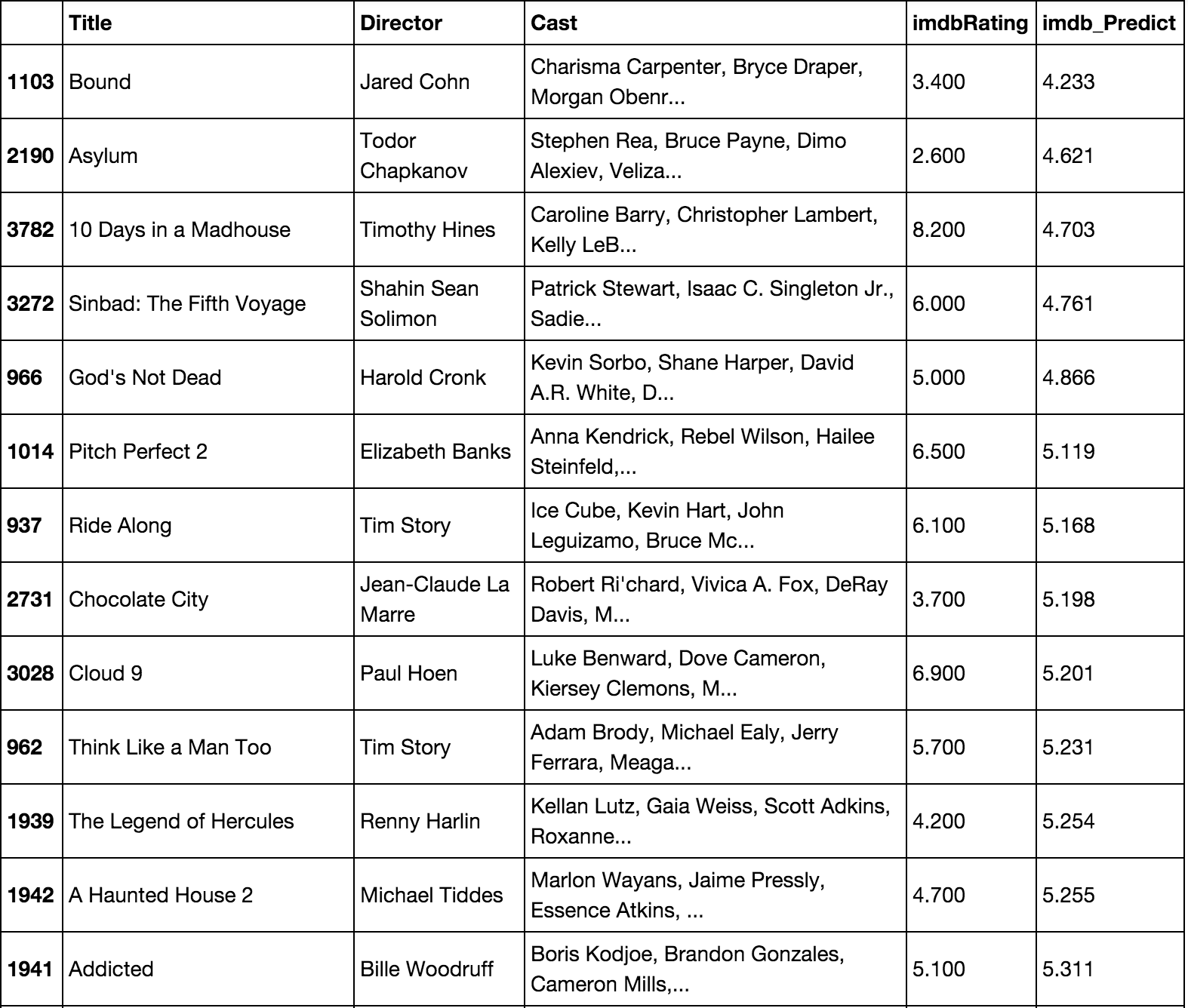
As well as the model's predicted biggest flops (sorry Madhouse!):

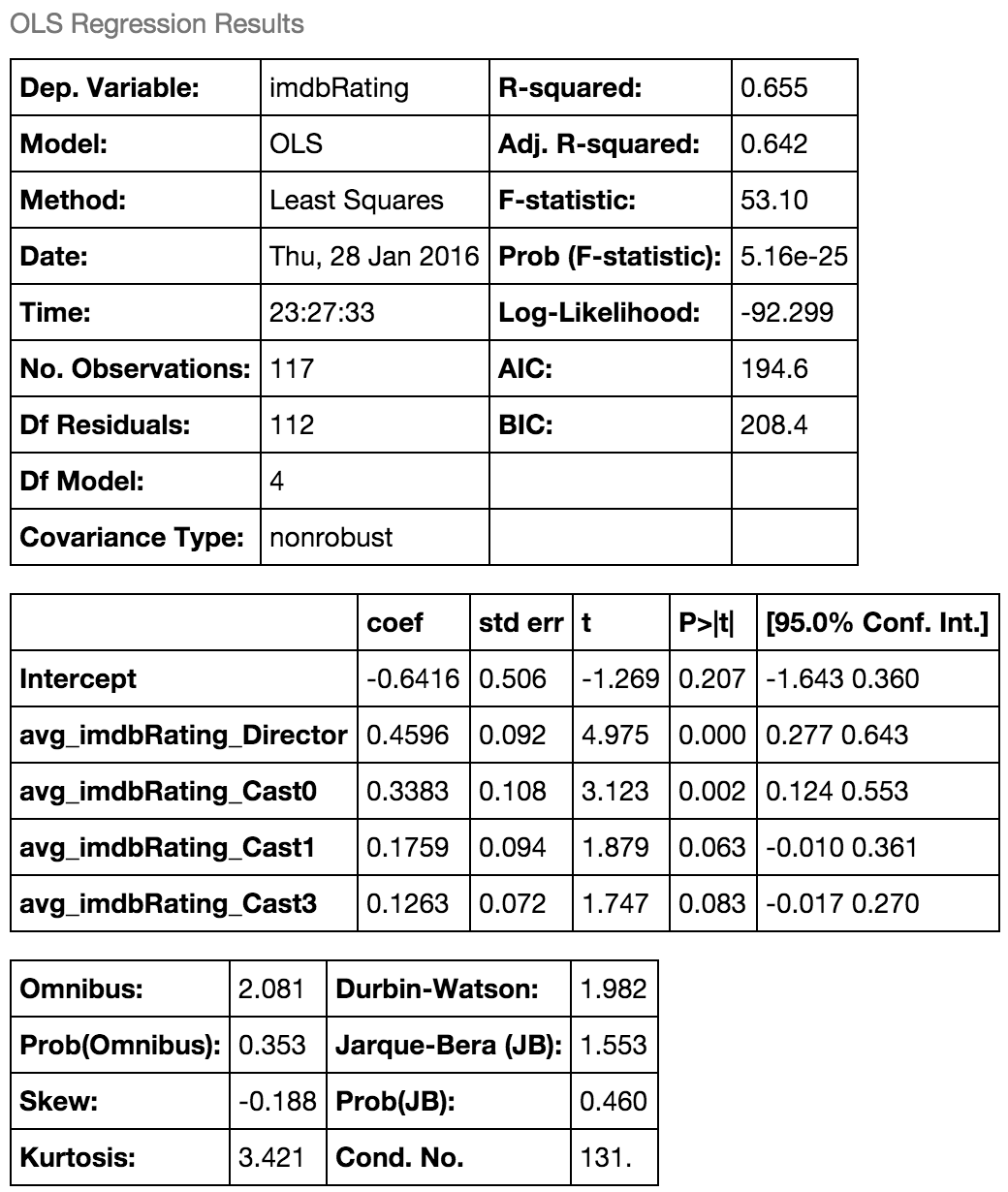
Finally, the full results of the linear regression are shown below: